Theorem of parallel transversals

Last updated 2023.03.13 Edit Source

• Math
• Geometry

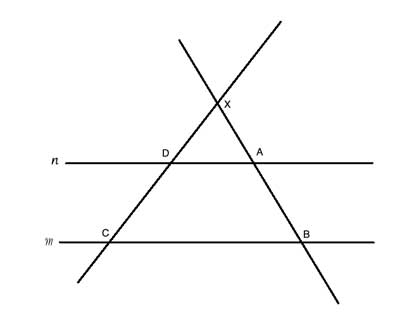
$\Delta XBC \sim \Delta XAD$ ← central similitude with center $O$

Theorem of transversal segments

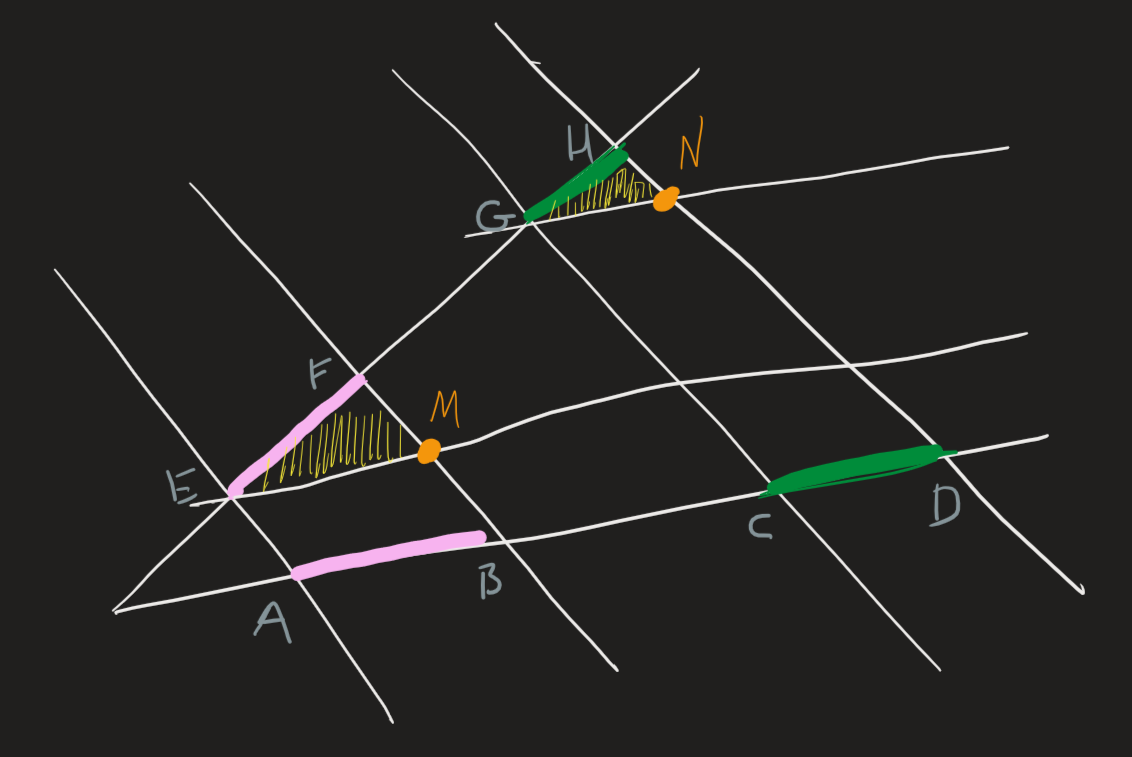
$$\frac{AB}{CD}=\frac{EF}{GH}$$

1. assume that $EF=GH$
2. **we try to show that $AB=CD$**T
3. draw parallels with the $AD$ arm through $E$ and $G$
4. we obtain $\Delta EMF$ and $\Delta GNH$ű
5. $\Delta EMF \cong \Delta GNH$, since
   1. $EF=GH$
   2. $\angle FEM=\angle HGN$
   3. $\angle EFM = \angle GHN$
6. $\implies EM=GN$
7. we can see that $ABME$ and $CDNG$ are parallelograms, therefore $CD=GN$ and $AB=EM$
8. $\implies AB=CD \implies \frac{AB}{CD}=\frac{EF}{GH}(=1)$

if $EF\neq GH$, then they can be cut into equal-sized pieces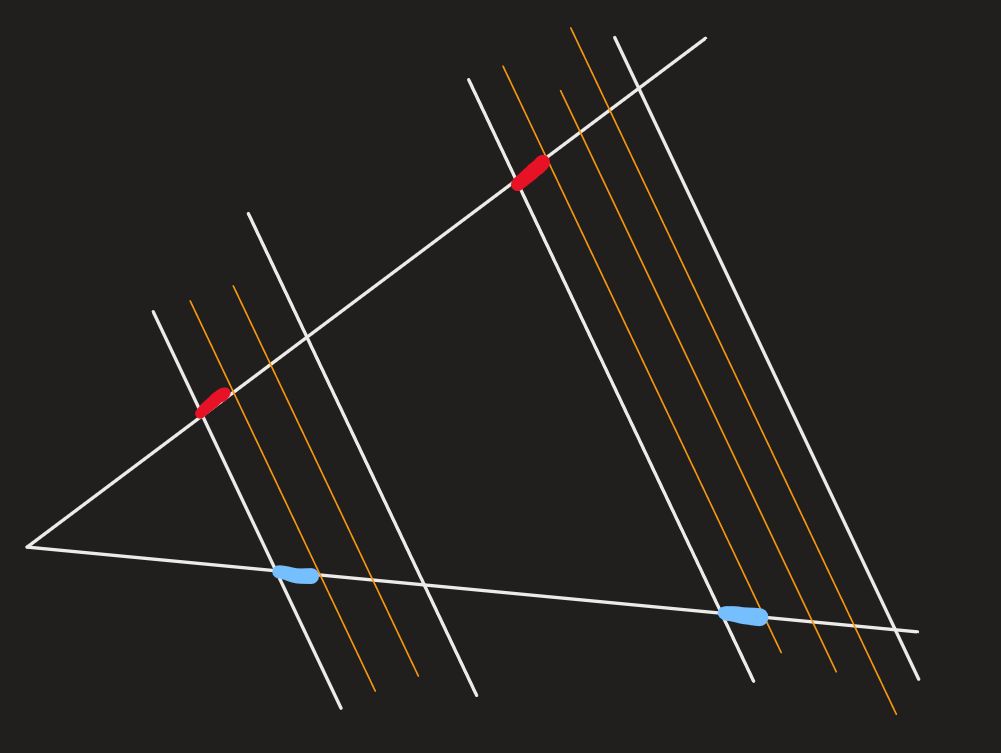

9. there is an equal number of RED and BLUE segments on the arms
10. by the above $\frac{AB}{CD}=\frac{EF}{GH}$